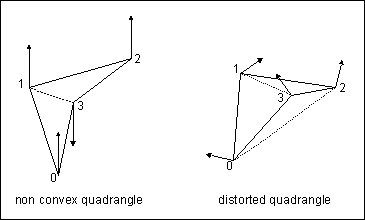
The program splits quadrangles which are not convex or too much distorted in 3D into triangles. This is neccessay because some other algorithms wouldn't work properly if this is not done.
The first task is to determine if a quadrangle has to be split into triangles. Second it is neccessary to find out where the quadrangle has to be split (there are two possibilities).
Both problems can be solved with the following algorithm:

First normal vectors of all points must be calculated.
The normal vector of point i is calculated performing the cross product
of vector v and w where v= point ((i+1) modulo 4) - point i and w= point
((i-1+4) modulo 4). This means the vectors v and w are defined by the edges
of point i. E.g. the normal vector of point 3 is defined by the cross product
of vector (point 0 - point 3) and vector (point 2 - point 3).
Note: all normal vectors must be calculated using the same order of v and
w in the cross product, otherwise comparing these vectors is useless.
Now the angles between the normals located on opposite sides of the
diagonals must be calculated:
a02 = angle between the normal of point 0 and the normal of point
2
a13 = angle between the normal of point 1 and the normal of point 3
The rest of the algorithm is simple. If the angle a02 or a13 is greater
than a specified value (can be set with the option -s,
default is 10 degree) then the quadrangle must be split. The quadrangle
is split so that the angle between the resulting triangles is minimal.
So if a02>a13 the quadrangle will be split at diagonal 0-2 else it will
be split at diagonal 1-3.
In the right half of the picture above the angle between the normals
of point 1 and point 3 is greater than the other so the quadrangle
will be split at diagonal 1-3.
The clou of the algorithm is that it can also handle non convex polygons. If a quadrangle isn't convex then the angle between the normals of the points at the diagonal where it has to be split is great. If the quadrangle is plane this angle is 180 degree.
In the left half of the picture above you can see a plane non convex quadrangle. The angle between the normals of point 1 and 3 is 180 degree and the angle between the normals of point 0 and 2 is 0 degree. So the algorithm splits the quadrangle at diagonal 1-3.