For generating the next LOD, leaf nodes of an octree will be combined into parent nodes. The type of the parent nodes will be changed from intermediate to (quasi) leaf. This will be done by changing the lod variable in the node from -1 to the number of the next LOD. Further the data of these parent nodes will be set to the data of the representatives selected out of the leaf nodes. So algorithms are necessary for selecting a representative out of a cluster of coordinates:
Basically the algorithms are calculating an errorfactor for each coordinate in the cluster. The errorfactor determines the error that will occur if this coordinate will be selected as representative. Then the errorfactors will be normalized to the intervall [0,1]. The program uses a weighted mean of the errorfactors calculated by the algorithms: errorarea, errorvolume and weightedmean for selecting the best representative. The weights for these three algorithms can be changed with the commandline options -1, -2 and -3.
This algorithm calculates for each coordinate in the cluster the change
of the area of all involved faces that will occur if this coordinate will
be selected as represent. The involved faces are that faces which uses
least one coordinate of the cluster. Each coordinate has a list of faces
which uses this coordinate. So the involved faces can be determined.

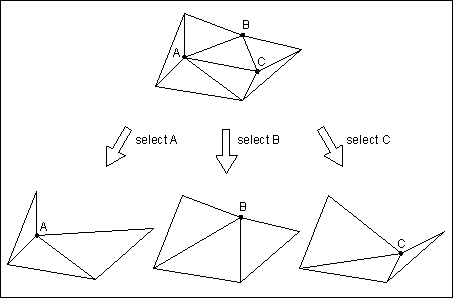
The picture above shows what will happen to the involved faces of a cluster of three points if A, B or C is selected as the representative. If the errorarea algorithm is used B will be selected because in this case the change of the area of the involved faces is zero. So you can see that this algorithm is good for preserving the contour of an object. Also for other reasons this algorithm is the best of the algorithms described here.
This algorithm selects one coordinate of the cluster and calculates the errorfactor for this coordinate as the sum of volumes. These volumes (tetraeders) are calculated for each involved face and are defined as follows:
The base of the volume is defined by the area of the old face and it's top is defined by the representative of the cluster. If none of the vertices of a face are mapped to the selected representative of the cluster the volume is zero. Quadrangles will be threated as two triangles for this calculation.
The involved faces are that faces which uses least one coordinate of the cluster. Each coordinate has a list of faces which uses this coordinate. So the involved faces can be determined.
Disavantage: The algorithm alway returns zero if all coordinates in the cluster are in the same plane. So this algorithm is only usefull in combination with another.
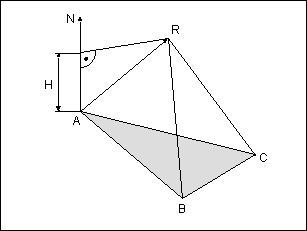
In the picture above R is the representative of the coordinate A in the next LOD. This means the face ABC is mapped to RBC in the next LOD. No matter if one, two or all three vertices of an triangle are mapped to the selected representative the volume defined by ABCR is always a tetraeder.
The volume of such a tetraeder is calculated as follows:
First the area of the old face ABC must be calculated. The volume of
the tetraeder is then (area of ABC)*H/3. For H it is necessary to calculate
the normal vector N of the old face ABC and e.g. the vector AR. Then H
can be calculated using the cosinus of the angle between the vectors N
and AR.
This Algorithm is very simple and the results are not very good.
First the algorithm calculates a weighted mean value of all coordinates
of the cluster. The weight of a coordinate is defined as follows: if the
coordinate is already a representative then the weight is the count of
all coordinates whose representative is this coordinate. If a coordinate
isn't a representative then it's weight is 1.
The errorfactors of the points in the cluster are simply the euclidean distances to the mean value calculated above.
The LOD generation algorithm for IndexedLineSet nodes uses only this selection algorithm because the other two works only with faces.