Details

Type

  • Bachelor Thesis
  • Student Project
  • Master Thesis

Persons

1
Workgroup
Rendering and Modeling

Description

Signed distance functions (SDF) can represent 3d models as distance values to the surface, commonly defined at each point in a uniform 3d grid, and are often used in neural models or as output from scans.  Due to the large size of scans and cubic complexity, these are often represented as a truncated variant that only keeps these distance values close to the surface, as a truncated SDF (TSDF), e.g., KinectFusion [1]. However, sensed samples are usually contaminated with noise, and this is not handled or only by oversmoothing on the already aggregated (T)SDF without considering individual sensor noise properties of the samples. By representing these noise properties in the (T)SDF, we aim to reconstruct a more faithful surface, bound by guarantees, and recover sharp features better.
 

Tasks

  • integrate depth images from a sensor (time-of-flight or LIDAR) using a suitable open source SLAM framework, e.g., OKVIS2-X [2], and store the probability density functions (PDFs) of the samples
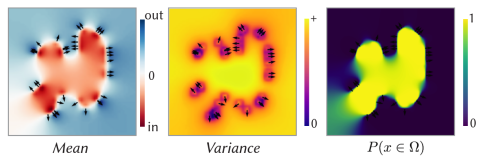
  • aggregate the Gaussian distribution (mean, variance) at corners of a regular sparse grid to a probabilistic SDF (PSDF) - as the SLAM framework does for the TSDF values, which correspond to the mean only
  • evaluate this PSDF by reconstructing a mesh from it,, comparing classic SDF reconstruction (e.g., Marching Cubes) with a sharp feature reconstruction method that we will provide, both with virtual-3d-scanner synthetic scans from a 3d model to measure the error and show results with real-world scans
     

[1] https://www.microsoft.com/en-us/research/publication/kinectfusion-real-time-3d-reconstruction-and-interaction-using-a-moving-depth-camera/

[2] https://arxiv.org/html/2510.04612v1

Image credit: S. Sellan and A. Jacobson. “Stochastic poisson surface reconstruction”. In: ACM Transactions on Graphics (TOG) 41.6 (2022).

Requirements

  • Knowledge of C++ (Python a bonus)
  • Knowledge of English language (source code comments and final report should be in English)
  • Bonus for experience with CUDA or geometry processing

Environment

Standalone C++/CUDA application (platform-independent, tested on Linux, Windows)

A bonus of €500/€1000 if completed to satisfaction within an agreed time-frame of 6/12 months (PR/BA or DA)

Responsible

For more information please contact Stefan Ohrhallinger.