Speaker: Hiroyuki Sakai
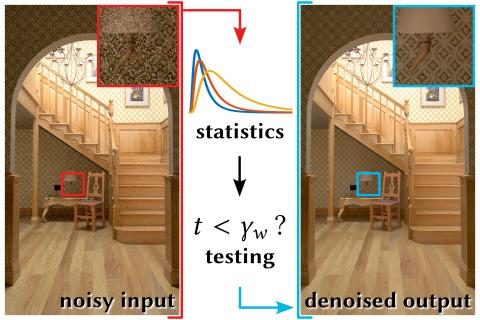
The stochastic nature of modern Monte Carlo (MC) rendering methods inevitably produces noise in rendered images for a practical number of samples per pixel. The problem of denoising these images has been widely studied, with most recent methods relying on data-driven, pretrained neural networks. In contrast, in this paper we propose a statistical approach to the denoising problem, treating each pixel as a random variable and reasoning about its distribution. Considering a pixel of the noisy rendered image, we formulate fast pair-wise statistical tests—based on online estimators—to decide which of the nearby pixels to exclude from the denoising filter. We show that for symmetric pixel weights and normally distributed samples, the classical Welch t-test is optimal in terms of mean squared error. We then show how to extend this result to handle non-normal distributions, using more recent confidence-interval formulations in combination with the Box-Cox transformation. Our results show that our statistical denoising approach matches the performance of state-of-the-art neural image denoising without having to resort to any computation-intensive pretraining. Furthermore, our approach easily generalizes to other quantities besides pixel intensity, which we demonstrate by showing additional applications to Russian roulette path termination and multiple importance sampling.