Speaker: Ludwig Weydemann
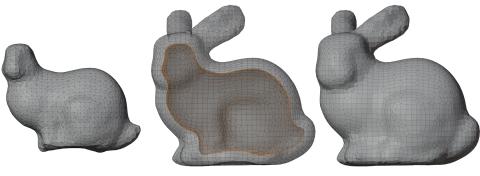
Offset surfaces are fundamental in computer graphics applications, such as computer-aided design or tool-path generation. However, generating them while preserving geometric details and handling self-intersections remains challenging, particularly for surfaces with sharp features. This thesis presents a robust method for non-uniform offset surface generation, extending volumetric, feature-preserving uniform offset approaches to allow per-vertex control over offset distances. This enables greater flexibility in handling complex geometries and user-defined specifications.
To achieve a smooth distribution of offsets across the input mesh, the method introduces a Radial Basis Function interpolation combined with Dijkstra-based distance propagation. The method supports the extraction of both inner and outer offset components through an octree data structure and a modified Dual Contouring algorithm adapted for non-uniform distances, ensuring accurate and manifold surface generation.
This approach's adaptability and robustness are demonstrated across diverse input models with varying offset assignments. They showcase successful extraction of inner and outer components and the ability to capture localized asymmetries while preserving geometric integrity.