Programmdokumentation
Datenstruktur:
Die XML-Dateien der Vessel Centerline Trees wird mit libxml2 geparst und in eine für uns gut verarbeitbare Datenstruktur importiert.
Wir halten uns dabei stark an die Struktur im XML-File und unterteilen den Baum in einzelne Segmente die jeweils aus einem Anfangs- und Endkontrollpunkt bestehen. Wenn das Segment nicht interpoliert wird, gibt es zwischen den Kontrollpunkten mehrere Segmentpunkte.
Bidirektionales Sampling:
Das down sampling ist ein Verarbeitungsschritt, welcher nur den Inhalt, jedoch die Datenstruktur selbst verändert. Das hat uns ermöglicht, diesen Schritt erst später einzubauen um uns zuerst mit dem Hauptteil der Meshgenerierung zu beschäftigen.
Das Sampling wird für jedes Segment getrennt gemacht. So kann man sicherstellen, dass die Verbindungspunkte, die Kontrollpunkte, zwischen den Segmenten sich nicht verändern und keine Löcher entstehen.
Das Sampling-Verfahren beruht auf folgender Regel: Ein Segmentpunkt wird dann behalten, wenn die folgende Bedingung gilt:
Die Krümmung κ wird dabei mit einer Approximation der
Kurve berechnet.
Sollte ein Segmentpunkt diese Bedingung nicht erfüllen, dann wird
der Punkt 
genommen, der diese Bedingung erfüllt. Als
Ergebnis wird das Mittel von und 
genommen.
Das Sampling endet, wenn
erfüllt ist, wobei 
der Samplingpunkt
vom Anfang kommend und 
der Samplingpunkt
vom Ende kommend ist.
Generierung des Meshes:
Die Generierung des Meshes wird in der Klasse „Mesh.cpp“ durchgeführt. Hier wird die Funktion „calculate Mesh“ aufgerufen, welcher ein Zeiger auf dem Root-Node übergeben wird.
Vorberechnungen
Bevor das Mesh generiert wird, war
es notwendig mehrere Vorverarbeitungsschritte durchzuführen. Zuerst haben wir
für jede cross-section eines Segments (segment points + control points) die
Normalvektoren und die Richtungsvektoren berechnet. Die Richtungen werden als
normalisierte Differenz zwischen den einzelnen Centerline-Punkten
berechnet:
Die Normalen wurden mit Hilfe der folgenden Formeln berechnet:
Die Berechnung der Richtungs- und Normalvektoren findet in der Funktion „calculateDirectionsNormals“ statt. Diese berechnet zuerst die beiden Vektoren für den Start Node und ruft anschließend die Funktion „calculateDirNorm“ auf, welche die Richtungsvektoren und Normalvektoren für alle Segment Points berechnet. Anschließend werden die beiden Vektoren noch für den End Node berechnet. Die Funktion „calculateDirectionsNormals“ ist eine rekursive Funktion, die sich selber immer wieder aufruft, bis das Ende des Vessel Trees erreicht ist.
Als nächster Schritt werden die Durchschnittsnormalen an den Verzweigungen berechnet. Hierfür werden für jede Verzweigung der Richtungsvektor des End Node des eingehenden Segmentes und die Richtungsvektoren aller Start Nodes, welche mit dem eingehenden Richtungsvektor einen Winkel kleiner als 90° einschließen, berücksichtigt. Anschließend werden der Richtungsvektor am End Node des eingehenden Segmentes, sowie die Richtungsvektoren aller Start Nodes der von der Verzweigung wegführenden Segmente, durch den Durchschnittsnormalvektor ersetzt. Die Berechnung der Durchschnittsnormalen wurde in der Funktion „averageNormals“ für alle Branchings durchgeführt.
Nach der Berechnung der Durchschnittsnormalen wurde der Up-Vektor für jede Cross-Section
berechnet. Hierfür wurde zuerst für den Start Node
des ersten Segmentes ein Up-Vektor normal auf dessen
Richtungsvektor gewählt. Der Up-Vektor wird
anschließend über alle Cross-Sections des gesamten Vesseltrees weitergegeben. Hierzu wird der Up-Vektor 
auf die Normalebene der nachfolgenden
Cross-Section, welche durch dessen Normalvektor 
und Mittelpunkt 
definiert ist,
in die Richtung 
projiziert und anschließend normiert. Die
Berechnung der up-Vektoren wird in der Funktion „calculateUpVektors“ durchgeführt.
Generieren des Meshes
In einem rekursiven Verfahren entsteht ein Mesh,
welches 2 Kontroll-/Segmentpunkte mit 4 Patches (als
rechteckiges Rohr) verbindet. Die Verbindung zweier solcher Punkte wird Sektion
genannt.
Da das Verfahren sehr gut rekursiv implementierbar ist, muss die
erste Sektion des Baums gesondert behandelt werden. Diese wird mit der Funktion
tileTrivially() erzeugt. Diese Funktion verwendet den
errechneten Up-Vektor der beiden Punkte und erzeugt
dadurch 4 Patches.
Der Up-Vektor zeigt zu Beginn in
Richtung des ersten Vertices 
.
Daher ergibt sich der Vertex folgendermaßen
Um den Vertex 
zu erhalten muss nun der Up-Vektor um 90 Grad
um den Richtungsvektor der cross-section gedreht werden und anschließend die
Berechnung aus Formel 6 durchgeführt werden. Die selbe
Prozedur wird noch weitere zwei Mal wiederholt um die beiden noch fehlenden
Vertices 
und 
zu erhalten (siehe Abbildung 1).
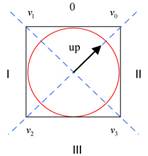
Abbildung 1: Definition des up-Vektors
Danach wird die Funktion tileTree()
mit dem aktuellen Segment aufgerufen. Diese Funktion erzeugt zuerst Patches für alle Sektionen die sich nicht verzweigen (alle
bis auf die letzte Sektion) mit der Funktion tileTrivially()
wie oben beschrieben.
Vor Bearbeitung der letzten Sektion müssen alle an das Ende
anknüpfenden Segmente in Forward- und Backward-Branches eingeteilt werden. Diese Klassifizierung
funktioniert so, dass die Richtungsvektoren der Anfangskontrollpunkte der
ausgehenden Segmente mit der Richtung des Endkontrollpunkts des aktuellen
Segments verglichen werden. Zeigen diese nicht voneinander weg, ist das Segment
als Forward klassifiziert, ansonsten als Backward.
Gibt es nun keine Backward-Segmente, kann die letzte
Sektion mit tileTrivially() berechnet werden,
ansonsten wird jedes der Backward-Segmente in einen
Quadranten (normal zur Richtung der letzten Sektion) eingeteilt. Jeder dieser
Quadranten wird dann mit der Funktion tileJoint() behandelt.
In tileJoint() wird folgendes getan:
Hat ein Quadrant keine Branch-Segmente, wird diese
Seite mit einem Patch verschlossen. Gibt es jedoch Branch-Segmente,
wird das Segment N, dessen Richtung am geradsten zur
Richtung des Quadranten ist aus dem Set der anderen Segmente entfernt. Die
restlichen Segmente dieses Quadranten werden nun in Quadranten relativ zu N
eingeteilt. Für jeden Quadranten wird nun die Funktion tileJoint()
aufgerufen. Schließlich wird ein Transition-Patch zwischen dem Segment, dessen
Quadrant gerade bearbeitet wird und N erstellt.
Nachdem nun die Backward-Segmente
bearbeitet wurden, können die Forward-Segmente bearbeitet werden. Hier wird in tileTree() das geradste Segment
im Verhältnis zum Vektor des gerade bearbeiteten Segments ausgewählt. Die
restlichen Segmente werden in Quadranten eingeteilt und mit tileJoint()
verarbeitet. (Das ist der Grund, wieso die erste Sektion im Baum extra
behandelt wird)
Am Ende der Funktion tileTree() wird
jedes ausgehende Segment (Forward und Backward) tileTree aufgeworfen um den Baum weiter durchzugehen.
Adaptive Subdivision:
Das Adaptive Subdivision wird in der Funktion „Subdivide“ in der Klasse „Adaptive Subdivision“ durchgeführt. Hier wird für jedes Triangle geschaut, ob es eine Krümmung hat die größer als ein vorgegebener Schwellwert ist. Wenn der Schwellwert überschritten wird, wird das Triangle in 4 neue Triangles geteilt, andernfalls wird das Triangle als „tagged“ markiert. Dies wird für alle abgespeicherten Triangles durchgeführt. Für das Berechnung der Krümmung wurde dieselbe Methode wie im Bidirektionalen Sampling verwendet.
Anschließend wird für alle „tagged“ Triangles geschaut, ob Nachbardreiecke geteilt wurden. Je nachdem wie viele benachbarte Triangles geteilt wurden, wird das Triangle in 2,3 oder 4 neue Triangles geteilt. Abbildung 2 verdeutlicht dies.
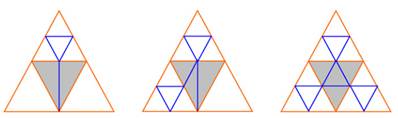
Abbildung 2: von rechts nach links: Fälle, in denen 1 Nachbar,
2 Nachbarn und 3 Nachbarn geteilt wurden
Die Funktion ruft sich anschließend rekursiv so lange wieder auf, bis die Abbruchbedingung erreicht ist. Als Abbruchbedingung wählten wir eine vorgegebene Anzahl an Funktionsaufrufen. Um das Adaptive Subdivision zu verbessern, sollte die Funktion so lange durchgeführt werden, bis kein Triangle eine Krümmung besitzt, welche den Schwellwert überschreitet.
Rendering:
Für das Rendering der Daten wurde die Engine, die für die VU „Echtzeitgraphik“ verwendet wurde, angepasst. Wir haben das Rendern der Daten mit Hilfe von DirectX 11 durchgeführt. Unsere Triangles haben in allen Vertices dieselben Normalen für die Lichtberechnung. Alle Triangles werden mit ambienten, diffusen und specular Licht gerendert. Wir haben uns weiters dazu entschlossen keine Textur zu verwenden.
Mit den Pfeiltasten kann man sich durch das Programm bewegen und mit der Maus kann man sich im Programm drehen.
Anmerkungen:
Da unser Programm leider noch sehr fehlerhaft ist, werden wir bis zur Präsentation noch eine verbesserte Version hochladen. Ebenso werden wir mit dem verbesserten Programm noch einige Screenshots in die Dokumentation einfügen.
Literaturverzeichnis
E. Calabi, P. O. (1998). Differential and numerically
invariant signature curves applied to object recognition. Int J Comput
Vision.
Jianhuang Wu, R. M.
(2010). Curvature-dependent surface visualization of vascular structures.
P.Felkel, A. K. (kein
Datum). SMART - Surface models from by-axis-and-radius-defined tubes.