Implementation: Gaussian KD-Trees for Fast High-Dimensional Filtering

Matthias Labschütz, e8971103@student.tuwien.ac.at

In image processing, filtering is typically based on filtering a 2 dimensional grid (image). Grids are more memory efficient than storing explicit points (1 value per point instead of dimensionality + 1 values). Nevertheless, the effort and data-space requirement increase exponentially in the dimension if an evenly spaced grid is used to represent the data. Even non existing data points need to be filled with a value inside a grid.

In [1], applications such as Bilateral filtering of RGB values, non local means denoising and geometry filtering are suggested. In the following implementation, the Bilateral filter is implemented for 2d greyscale values. This is the most basic application of the proposed method. The program was written with the goal of extending the filtering process to 3 dimensional volumes, which explains certain details in the implementation. The algorithm was implemented on the CPU (also due to the limited memory on GPUs).

In the following, the algorithm is summarized; the implementation presented and in the end a discussion explaines why certain choices were made.

The Algorithm

Bilateral filtering is an edge-preserving Gaussian blur, see Figure 1. To realize this, the values are weighted depending on their distance in intensity space. Bilateral filtering is a non-linear filtering process, in [2] a fast implementation of the Bilateral filter is proposed which increases the dimension of the space by an intensity axis (thus a 2d image is handled as a 3d volume). The advantage of this approach is that blurring can be realized by a Gaussian blur in higher dimensional space. Since the Gaussian blur is separable this can be done efficiently.

Figure 1: Noisy vs. Bilateral filtered image with a GKD-tree. Edges are retained in the filtered image.

The Bilateral filter with use of GKD trees executes the following steps (a 2 dimensional case is explained, this approach can be extended to higher dimensions):

1. Construction of a GKD tree: A 2d image is seen as a height-map in 3 dimensions. This 3d space is split during the creation of the GKD. The bounding box of the 3d space is recursively split in half along its largest extent. This is repeated until the diagonal of the bounding box is smaller than a sigma threshold. Every leaf node is assigned with a zero value and a three dimensional position in space.
2. Down-sampling (splatting): To store the appropriate values in the leaves and iteration over all points of the image takes place. At every image point a Gaussian query is executed to find the nearest leaf nodes and their weight, according to their distance. The pixel values are written to the leaf nodes and weighted.
3. Gaussian blur: The GKD is blurred with another query. Every leaf node of the tree propagates its value to the neighboring leaf nodes.
4. Up-sampling (slicing): Once again, for all pixel values the weighted values of nearby leaf nodes are gathered. This is the final blurred result.

Implementation

This section will also give an overview of the features and mechanisms that are implemented but not required for this particular application of the algorithm. 

User Interface

Elements of the user interface in Figure 2. Any '*.png' files contained in the 'data/' folder will be detected and show up in the file list to select from.

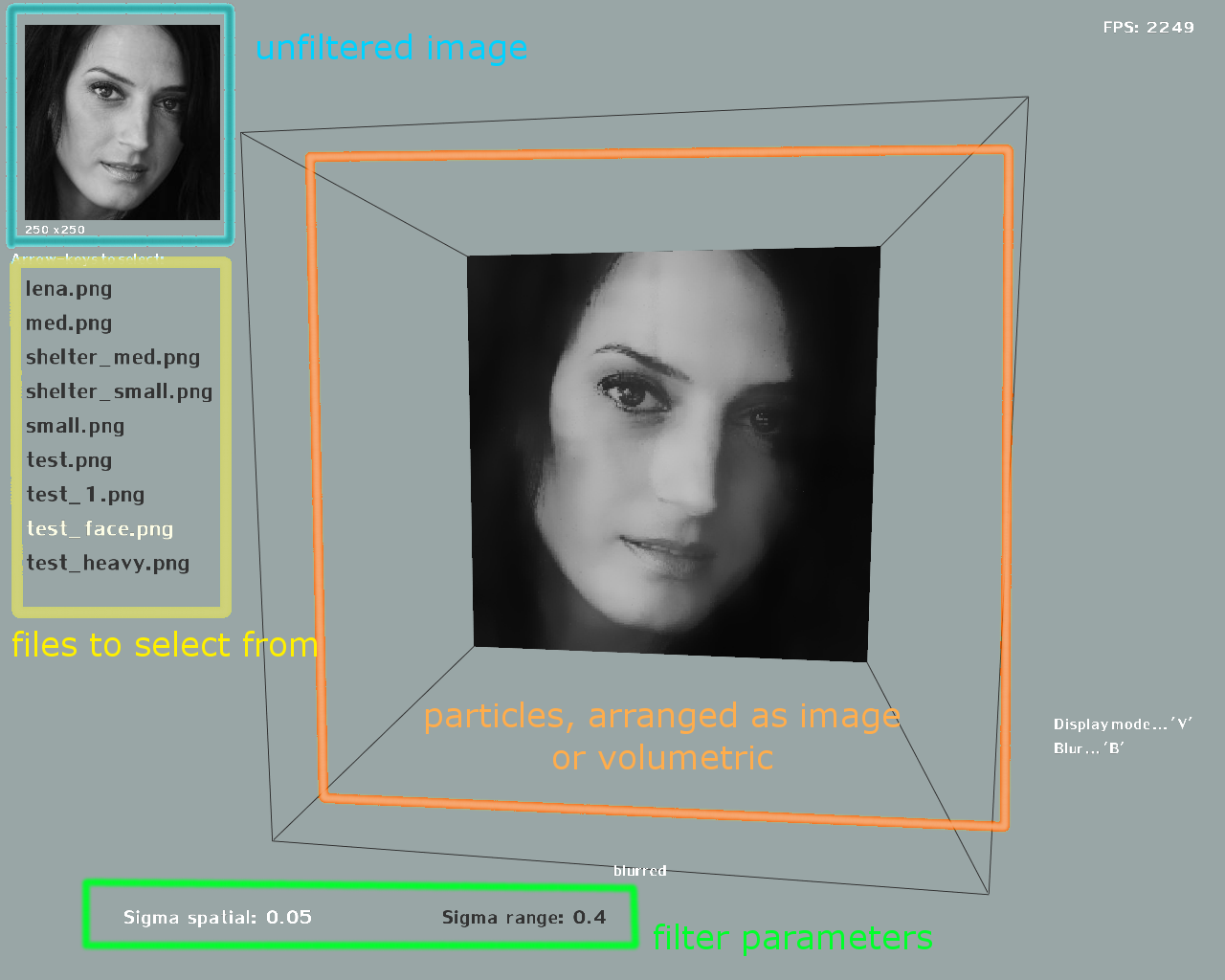
Figure 2: Basic user interface. The files can be selected with the arrow keys (up, down). Enter opens a file. B filters a selected file. Highlighted in green, two sigma values can be picked (use the number keys and backspace to modify the selected sigma value). V changes to volumetric view. (original image:Q. Yang et al., SVM for Edge-Preserving Filtering, http://vision.ai.uiuc.edu/?p=1460)

The data

The original data is split into a quad/octree until the leaf nodes are small enough to fit fully into memory (FileOctree, FileNode). The leaves are separate files on the hard-disk. The following algorithm works on this split up data structure.

Figure 3: Unfiltered Lena data-set in the 3d view.

The GKD Tree

Tree generation is done recursively on the CPU, which is slower, but more simple, than a parallelized iterative approach. The difficulty was to integrate the out-of-core data management. Ever iteration over all points of the currently considered volume require to read successive files from the disk. To minimize I/O operations the size of the data in the memory was meant to be minimized. The most efficient storage structure is the grid (with dimensionality one lower than the extended space due to the Bilateral grid approach). Instead of minimizing instructions, the data was handled as a grid structure in memory. Only when approaching the leaves the data gets small enough te be treat as a list of point (which is the most easy implementation).

Figure 4 shows a debug view of the kd-tree which was heavily used, but cannot be displayed in the release version without modifying the source code.

Figure 4: A partial visualization of the kd-tree of the Lena data-set. The small dark dots are the actual pixels displayed in a smaller size. The debug visualization of leaf nodes was fully removed from this version.

The queries are implemented as presented in [1]. For the normalization of the weights, the implemented approach was to sum all weights and normalize them per leaf node.

The final result overwrites the leaf files of the octree on the disk. Due to time restrictions the method to save the filtered image back to disk is not implemented yet.

Figure 5: Lena dataset after Bilateral filtering. The sigma values are to be seen in relation to the full data-set of [0..1]x[0..1].

Framework

Known bugs

• Stuttering controls on older processors due to basic multithreading (in this case, threads are executed sequentially in temporal chunks)

Discussion

The downside of the algorithm is its difficulty in implementation. Also the performance of this particular implementation is far from the original goal of high performance filtering. For high radius filters, the method performs better than for low sigma. The effort of a brute force filter algorithm increases in the radius with the power of the dimensionality. Due to importance sampling this workload is heavily reduced. For small kernels the kd tree needs to be split further, resulting in more leaf nodes and a higher computation cost.

The normalization of the weights needs to be confirmed or fixed (since this was not clear during implementation).

In the future it can be interesting to use the method for different goals (as originally intended) and to finalize the out-of-core approach.

References